【アルゴリズム】ワーシャルフロイド

また気づいたらこんな時間だ。

そろそろまともな時間に書けるような生活習慣にしたいものだ。

CreateJSの仕様に長い時間苦しんでおり、AquaTypographyの解説が出来ない（次までにバグが取れないようなら次の作品に行きます）

なので今回は競技プログラミングをやっていた経験から便利なアルゴリズムを紹介する。

ワーシャルフロイドとは？

全ノードの最短経路をO(N^3)で実現出来る素晴らしいアルゴリズム。

このアルゴリズムの特徴はなんと言っても数行で全てのノード間の最短経路が求められるところにある。

実際のコード

for(int k = 0; k < n; ++k)
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < n; ++j) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

え、この数行で全てのノード間の最短経路が求まるの？とびっくりした方も多いと思います。

はい、このコードでノード間の距離をしっかりと初期化していれば求まります。

初期化も含めたコードだとこんな感じ。

const int INF = 1e+6;
const int n = 100;
int d[n][n];
std::fill(d, d + n * n, INF);

for(int i = 0; i < m; ++i)
{
    // 本来なら何かしらの入力からノード間のパス情報を取得する
    const int from = pathInfo[i].from;
    const int to = pathInfo[i].to;
    const int distance = pathInfo[i].d;
    // 片方向、両方向のどちらでもワーシャルフロイド法は対応することが出来る
    d[from][to] = distance;
    d[to][from] = distance;
}

for(int k = 0; k < n; ++k)
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < n; ++j) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

これってどんな仕組みで動いているのか？

ワーシャルフロイドの仕組み

今回はこちらの画像を拝借する(参考:ゲーム制作の舞台裏 ダイクストラで最短経路探索)

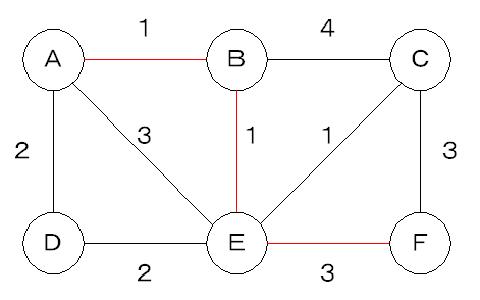
forループのi,j,kにはそれぞれ役割があり、

i:接続元ノード

j:接続先ノード

k:中間ノード

と、なっている。

• (i, j, k) = (A, B, E) の場合

AノードからEノードを通してBノードにアクセスした場合、A->B間の距離が短くなっていれば更新するが、

もちろんわざわざEノードを通さなくても、A->Bは既に1となっているのでこの結果は採択されない。

では、次の例を見てみよう。

• (i, j, k) = (B, C, E) の場合

今度はB->E->Cという経路を通ることで、B->E間の距離は2となり、現在の距離よりも小さいので更新する。

これでB->Cの最適な距離が求まった。

さて、この結果を保持した状態で次はこのような例でやってみよう。

• (i, j, k) = (C, A, B)の場合

本来ならC->B->Aという通り方をすれば、4 + 1 = 5という距離が計算される。

しかし、事前にB->C間の最短距離が求められているため、2 + 1 = 3という値になる。

本来ならC->Aというパスは存在しないが、求められた最短経路をパスとして構成されるようになる。

この繰り返しで結果的に全てのノード間のパスが構成され、最短経路が求まっている訳だ。

最後に

最短経路問題はアルゴリズムの中でも頻繁に使うテクニックのひとつなので、

簡単に覚えられるワーシャルフロイド法を覚えてみても損はない。

中間ノードを順次変えながら全てのノードの組み合わせで最短距離が計算されるのだが、

そのコードがあの数行のシンプルなコードに収まるのは考えた人の着眼点には敬意を表する。

以上、アルゴリズム講座でした。